본 글에서는 중3 수학 목차를 확인해 보고 현재 중학교 3학년 입장에서 그리고 앞으로 고등학교 수학 공부를 준비하는 입장에서 어떤 식으로 각 단원을 공부해야 하는지 수학을 가르치는 저의 입장에서 설명해 보고자 합니다.
중학교 수학 목차를 통한 완벽한 공부법 (실제 경험 기반)
이번 글에서는 수학이란 과목의 목차가 왜 중요한지를 설명하고 그 목차를 활용해 어떤 식으로 수학 공부를 해야 하는지에 대해서 설명해 드리도록 하겠습니다. 중학교 수학은 고등학교 수학의
honeyreviewer.com
글을 읽으시기 전에 제가 쓴 이 글을 읽고 오시는 것을 강력하게 추천합니다. 제가 강조하는 가장 본질적인 부분을 담았고, 아랫글을 이해하시는데 큰 도움이 되실 겁니다.
중3 수학 목차

전체적으로 대수적인 파트가 많이 포함된 3학년 1학기 내용입니다. 만약 대수적인 파트라는 말이 와닿지 않으시면 위에 링크 달아놓은 글을 꼭 읽고 와주시기를 바랍니다. 대수적인 파트는 고등학교 수학 기준 '미적분'으로 이어지는 내용들입니다. 미적분뿐만 아니라 고1, 고2, 고3 내내 배우는 모든 내용 여기저기에서 기본적인 계산이나 생각하는 과정들을 배웁니다. 이 내용을 공부하는 데 있어 가져야 할 기본적인 마인드는 '글 혹은 그림 등으로 쓰여 있는 내용을 식으로 표현하거나 식으로 쓰여 있는 내용을 글로 읽을 수 있는 능력을 기르자' 입니다. 수학이란 학문은 자연 세계에 존재하는 현상들을 수학적인 기호나 숫자 등을 통해 논리적으로 표현하는 학문입니다. 이 점을 명시하고 공부하시면 큰 도움이 되실 겁니다. 너무 두루뭉술한 얘기일 수 있으니, 단원별로 어떻게 학습하면 좋을지 자세하게 설명하도록 하겠습니다.
1. 제곱근과 실수
이 단원은 앞으로 고등학교에 있을 연산에 사용할 도구들에 대한 공부를 하는 단원이라고 생각하시면 편합니다. 이 전까지는 주로 자연수, 정수, 유리수(소수나 분수 등)를 대상으로 계산을 진행했다면 앞으로는 이 범위를 '실수'까지 늘린다고 생각하시면 됩니다. 학생들은 학년이 올라가면서 원래는 자연수만 가지고 계산하다가 정수, 유리수로 계산의 범위가 늘어나는 것을 경험하셨을 겁니다. 이와 똑같은 흐름으로 '실수'라는 범위로 한 번 더 범위가 늘어난다고 생각하시면 됩니다. (고1이 되시면 '복소수'로 마지막으로 수의 범위가 늘어납니다) '실수'는 유리수와 무리수를 합친 범위의 수라고 생각하시면 됩니다. 그래서 자연스럽게 '무리수'에해서 공부하게 됩니다. 자세한 개념 설명을 해드릴 수는 없기에 예시를 들자면 가장 대표적인 무리수는 원주율 파이(3.141592...)이 있습니다. 그리고 우리가 가장 많이 사용할 무리수는 일명 '루트'라는 기호가 들어간 제곱근이라는 친구들입니다.
정리하자면 '실수'로 계산의 범위를 확장하기 위해 대표적인 무리수인 '제곱근'에 관해서 공부하는 것입니다. 더 나아가 루트가 들어간 식들을 가지고 저학년 때 배웠던 사칙연산, 곱셈 법칙들을 적용해 계산하는 훈련을 합니다. 루트라는 것 자체도 이해가 제대로 안되는 데 그걸 가지고 예전에 배웠던 여러 계산들과 응용하려니 학생들이 힘들 수밖에 없습니다. 이 부분에 대한 해결책을 포함해 공부 방법에 관해서 설명해 드리겠습니다.
(1) 실수, 무리수, 유리수, 정수, 자연수.... 이들의 포함 관계와 정의를 명확하게 아셔야 합니다.
심지어 고3이 되었는데도 수 체계에 대한 이해가 부족한 학생들이 있습니다. 이는 유튜브에만 검색해도 쉽고 깔끔하게 정리된 강의들이 많으니 참고해 주세요.
(2) 제곱근의 뜻이 무엇인지 정확히 이해하셔야 합니다.
4의 제곱근은 +2와 -2입니다. 하지만 제곱근 4는 +2 하나입니다. 제곱근을 제대로 이해하지 않으셨다면 이 이유를 설명하기 힘드실 겁니다. 제곱근은 '제곱해서 특정한 수가 되는 수'입니다. 제곱해서 4가 되는 수는 +2와 -2이지만, 제곱해서 2가 되는 수는 이전까지의 지식으로는 표현할 수 없습니다. 그래서 정의된 개념이 제곱근(루트) 입니다. 이에 대한 정확한 이해가 필요합니다. 그렇지 않으면 제곱근을 가지고 연산하는 건 그냥 대충 공식만 대입하는 노동에 가까운 행위가 됩니다.
또한 고등학교 수1 내용의 지수와 로그 단원은 '거듭제곱근' 개념에서 출발합니다. '제곱근'조차 명확하게 이해하고 있지 못하다면 '거듭제곱근'은 물론 그로부터 파생되는 개념인 '로그' 또한 외계어가 될 것입니다.
2. 다항식의 곱셈과 인수분해
학년이 올라가면서 어떤 문제를 볼 때 숫자보다 x, y 등의 문자가 많이 보이는 현상이 발생합니다. 계속해서 숫자 위주의 내용에 노출되어 있던 학생들은 상위권 학생이든 하위권 학생이든 거부감이 들 수밖에 없습니다. 그렇기에 이런 문자 위주의 식들과 친해지는 것이 중요합니다. 이에 대한 시작이 이번 단원인 다항식의 곱셈과 인수분해라고 할 수 있습니다.
숫자로 이루어진 식과 문자로 이루어진 식의 가장 큰 차이는 '항'이라고 생각합니다. 우리는 1 + 2 + 3 이라는 식을 보면 계산을 통해 '6'이라는 하나의 덩어리로 인식할 수 있습니다. 하지만 a + b + c라는 식은 a, b, c 각각이 뭔지 모르는 이상 하나의 덩이라가 아닌 a, b, c 세 덩어리로 인식할 수 밖에 없습니다. 이 덩어리를 '항'이라고 표현하고 이런 항이 두 개 이상 포함된 식을 다항식이라고 합니다.
이런 문자식의 특징 때문에 여러 현상이 발생합니다. 예를 들면 문자식에서 (1+2)*(1+2) 이라는 식은 그저 계산을 통해 9라는 사실을 알 수 있습니다. 하지만 (a+b)*(a+b)는 덧셈 계산이 안 되기에 (a+b)^2이라는 식을 배웁니다. 그렇기에 문자로 이루어진 식 중 특별하게 많이 등장하는 식들에 관해 공부하는데 이 식들을 '곱셈 정리' 식이라고 하고 이 곱셈정리를 반대로 생각한 개념을 '인수 분해'라고 합니다.
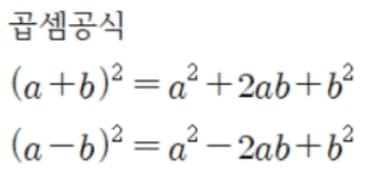
이제 다항식의 곱셈과 인수분해 단원에서 어떻게 공부해야 할지에 대해 설명해 드리겠습니다.
(1) 식을 무작정 외우지 말고, 식이 유도 되는 과정을 여러 번 반복 연습해 보자.
단순히 곱셈공식을 외우는 데 그치지 말고, 그 공식이 유도 되는 과정을 실제 계산을 통해 확인해 보는 연습이 중요합니다. 그래야 공식이 응용되었을 때 당황하지 않고 적용할 수 있습니다. 또한, 교과서에 제시된 공식들을 그대로 믿지 말고, '왜 이런 공식이 나온 거지?' 혹은 '이 공식은 정말 맞는 걸까?'라는 호기심을 갖고 탐구하는 것은 고등학교 혹은 대학교에 올라가서 할 공부를 생각해도 매우 바람직한 태도입니다.
(2) 인수분해의 뜻을 정확히 이해하고, 곱셈공식의 반대 과정이 인수분해임을 이해하자
인수분해, 말 그대로 인수로 분해한다는 뜻입니다. 그럼 '인수'란 무엇인지 여기서 나온 '분해'란 무엇인지 궁금증을 갖는 것이 바람직합니다. 비슷한 단어 중 '소인수 분해'라는 말도 있는데 그것과는 어떤 차이가 있는지도 비교해 가며 '인수분해'가 정확히 무슨 뜻인지 개념을 읽고 강의도 들으며 학생이 깊게 이해하는 것이 매우 중요합니다.
또한 곱셈공식의 '반대 과정'이라는 것도 중요합니다. 덧셈의 반대가 뺄셈, 곱셈의 반대가 나눗셈이듯 곱셈공식의 반대는 인수분해입니다. 인수분해 자체를 이해하는 것도 중요하고 곱셈공식의 반대라는 말이 무슨 뜻인지 이해하는 것도 중요합니다. 다행히도 이를 이해하는 것은 그저 식이 유도되는 과정을 관찰하면 비교적 쉽게 관찰할 수 있지만, 이 과정은 이후에 있을 수많은 '반대 개념'을 만났을 때 공부하는 태도를 만든다는 관점에서도 중요합니다. 함수와 역함수, 지수와 로그, 미분과 적분 등 앞으로 정말 많은 반대 느낌(?)의 개념들을 접하게 될 것입니다.
3. 이차방정식, 4. 이차함수
이차방정식 단원과 이차함수 단원은 중3 1학기 기말과정에 한꺼번에 포함되고 내용도 사실상 이어져 있는 것과 마찬가지니 한꺼번에 설명하겠습니다. 중학교 3학년 과정은 아무리 강조해도 모자라지 않을 정도로 중요한 개념들이 계속해서 등장합니다. '이차방정식과 이차함수' 단원 또한 마찬가지입니다. 학생들이 가장 먼저 배우는 방정식은 '일차방정식'입니다. 많은 학생이 이 일차방정식을 공부할 때는 비교적 큰 어려움을 겪지 않습니다. 하지만 이차방정식 단원은 소위 '수포자'가 가장 많이 발생하는 단원입니다. 그 이유는 우선 내용 자체가 어렵습니다. 일차식은 우리가 수도 없이 접해왔던 식이지만 이차식은 그보다 한 차원이 올라간 식입니다. 차원이 다르다는 표현이 딱 맞겠네요. 그렇기에 학생들은 내용 자체가 받아들이기 힘들어 당황하게 됩니다. 또한 호흡이 매우 깁니다. 지금까지는 한 단원 한 단원 차근차근 공부해 왔다면, 이차방정식은 앞에서 곱셈공식과 인수분해를 제대로 공부하지 않았다면 계산 자체가 불가능하고, 뒤쪽에 나오는 이차함수까지 내용이 이어지기에 부담감은 더 커집니다.
또한 이차함수 단원은 더 심각한 경우가 많습니다. 우선 이차방정식 단원에서 멘탈이 털릴 대로 털린 학생들이 그를 이용해 함수에까지 적용하는 이차함수 단원을 만나니 정신을 차리기 힘들겠지요. 하지만 이렇게 힘든 상황에도 불구하고 이차함수는 1학기 내용 중 가장 중요한 단원입니다. 고등학교 과정은 대부분 함수를 다루는 과정입니다. 고1 과정부터 '미적분'을 향해 달려가고 있는데, 이 미적분은 애초에 함수를 다루는 학문이기 때문입니다. 고등학교 수2 과정에서 주로 삼차함수, 사차함수에 대한 미적분을 다루는데 이차함수를 제대로 이해하지 못했다면 범접할 수 없는 어려움을 느낄 것입니다. 이는 삼차함수의 도함수는 이차함수, 사차함수의 도함수는 삼차함수... 이런 형태이기 때문인데, 쉽게 말해 이차함수를 알아야 삼차함수를 정의하고 이해할 수 있고 그 이후의 함수들도 똑같은 과정으로 이해할 수 있기 때문입니다. 그뿐만 아니라 이차함수는 미적분 단원 외에도 여러 단원에 직간접적으로 끊임없이 등장합니다. 사실 미적분을 포함한 고등학교 수학의 어려운 내용들을 못 하는 이유는 그 내용 자체가 어려운 이유도 있겠지만, 중학교 때 이차방정식~이차함수 단원을 제대로 공부하지 않아, 첫 단추부터 잘못 채운 경우가 많습니다. 그렇기에 더욱 제대로 된 공부가 필요하다고 강조하고 싶습니다.
(1) 수학을 긴 호흡으로 연결해 가며 공부하는 방법을 터득하세요.
어차피 고등학교에 올라가면 초등학교 때부터 공부했던 내용부터 고등학교 과정의 내용까지 전부 연결해 이해하고 적용해야 합니다. 그렇지 않으면 절대로 고득점을 받을 수 없습니다. 이에 이 단원을 공부하며 그 연습을 미리 하고, 적응하는 훈련이 필요합니다. 이차방정식 단원을 공부하며 앞에서 학습했던 곱셈공식과 인수분해를 자연스럽게 연결하고 또, 이 내용을 이차함수 단원까지 의식적으로 연결해 가며 공부하셔야 합니다. 고3 혹은 n 수생들을 가르치며 든 생각은 상위권 이상의 학생을 제외하고는 이차방정식과 이차함수를 정확히 연결해 공부한 학생을 본적이 거의 없습니다. 이게 제대로 되어 있지 않다면 더욱 어렵고 긴 고등학교 수학을 제대로 공부할 수 있을 리가 없습니다.
(2) 문제 풀이보다 개념에 더 집중해 주세요.
사실 앞 단원인 곱셈공식과 인수분해 단원까지는 개념을 대충하고 문제를 풀어도 그럭저럭 풀만할 수도 있습니다. 또, 문제를 통해서 개념을 깊게 이해되는 경우도 생기죠. 하지만 이차방정식 단원과 이차함수 단원은 개념 자체를 확실하게 이해하는 게 매우 중요합니다. 정말 과학고에 가야 해서 내신 성적이 필요하거나 올림피아드 등을 준비하지 않는 이상 그냥 문제만 풀어제껴서 내신 성적 조금 올릴 바에는 문제 풀이는 거의 하지 않고 내용을 이해하는 데에만 집중하라고 말씀드리고 싶을 정도입니다. 이차방정식을 확실하게 이해하고 그 '이차방정식'이 함수 형태로 표현되는 과정과 그로 인해 생기는 현상들을 끊임없이 관찰해 주세요. 이는 고등학교 과정에서 다루는 더 어려운 함수들을 탐구하는 힘을 길러줄 것입니다. 제가 앞서 설명해 드렸듯이 수학은 그림이나 글을 수학적 기호와 식으로 표현하거나 이를 반대로 하는 과정입니다. 이차함수에 대한 이해 없이 문제 위주 학습을 하는 것은 단순한 숫자놀음에 불과할 것입니다.
여기까지 중학교 3학년 1학기 목차를 통해 학생들이 어떻게 공부하면 좋을지에 대해서 이야기해 보았습니다.
댓글